Diagonals of a square array

The $5 \times 5$ array

contains $5^2 = 25$ dots, arranged in 5 rows and 5 columns.

We can view the array as consisting of a series of disjoint diagonals:

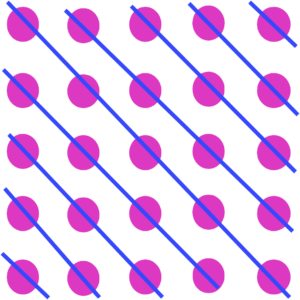
Counting the dots in the diagonals we get

$(1+2+3+4)+5+(4+3+2+1) = 5\times 5$

which, looked at another way, says

$1+2+3+4 = (5^2-5)/2$ .

Of course, there’s nothing special about 5: we can see by looking at an $11\times 11$ square array of dots that

$1+2+\ldots + 9 +10 = (11^2-11)/2$

and, more generally, if $n$ is any positive integer then

$1+2+\ldots + n-2 +n-1 = (n^2-n)/2$ .

Seeing a square array of dots as a series of diagonals is key to understanding, and proving, that

$1+2+\ldots + n-2 +n-1 = (n^2-n)/2$

for any positive integer $n$ .

This idea is a small, yet significant, step in awakening a developing mathematical brain.